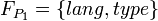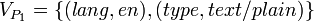Formal Definition
From WebLichtWiki
Contents[hide] |
Preliminaries
-
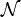 – a set of all the possible value names,
– a set of all the possible value names,
-
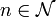 – a value name,
– a value name,
-
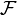 – a set of all the possible feature names,
– a set of all the possible feature names,
-
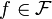 – a feature name,
– a feature name,
-
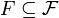 – a feature set,
– a feature set,
-
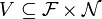 – feature/value relation, a set of
– feature/value relation, a set of 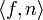 ordered pairs, i.e. a binary relation between
ordered pairs, i.e. a binary relation between 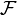 and
and 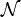 .
.
Example:
- F1 = {lang,type} – a feature set containing two feature names lang and type,
- V1 = {(lang,en),(lang,de),(type,text / plain) - feature/value relation contianig three ordered pairs.
Profile
A profile is a tuple 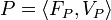 describing some input/output data for a web service:
describing some input/output data for a web service:
-
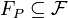 – profile features, a feature set of data features,
– profile features, a feature set of data features,
-
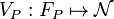 – profile feature/value map , a function from profile features to their values representing input data.
– profile feature/value map , a function from profile features to their values representing input data.
Example:
Input
A web service input is a tuple 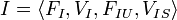
- input features
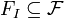 a set of features that must be present in the input of a web service,
a set of features that must be present in the input of a web service,
- input feature/value relation
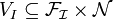 a relation representing possible values of the input features of a web service,
a relation representing possible values of the input features of a web service,
- user specifiable input features
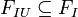 features that a user may specify,
features that a user may specify,
- input selected feature/value map
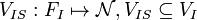 a total function mapping each input feature to its selected value.
a total function mapping each input feature to its selected value.
Example:
-
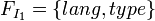 ,
,
-
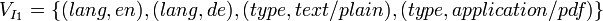 ,
,
-
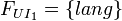 ,
,
- VIS = {(lang,en),(type,text / plain)}.
Output
A web service output is a tuple 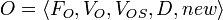
- output features
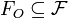 a feature set representing an output of a web service,
a feature set representing an output of a web service,
- output feature/value relation
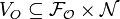 a relation representing possible values of the output features of a web service,
a relation representing possible values of the output features of a web service,
- output selected feature/value map
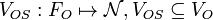 a total function mapping each output feature to its selected value.
a total function mapping each output feature to its selected value.
- input dependence map
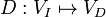 , where
, where 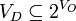 , such that
, such that 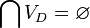 maps input feature/value pair to a set of dependent output feature/value pairs.
maps input feature/value pair to a set of dependent output feature/value pairs.
- new - a web service output does not include its input, i.e.
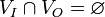 .
.
Example:
-
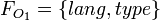 ,
,
-
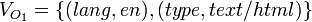 ,
,
- VOS = {(lang,en),(type,text / html)},
-
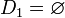 ,
,
- new1 = true.
Service
A web service chaining description is a tuple 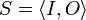 .
.
- input I a web service input,
- output O a web service output.
Chaining Requirements
- required input features
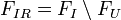 ,
,
- matching profile values
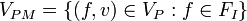 .
.
Example:
-
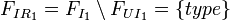 ,
,
-
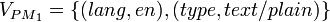 .
.
Match Function
A match function 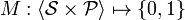 from a set of all the possible web service/profile tuples into zero or one. If the value is one then profile
from a set of all the possible web service/profile tuples into zero or one. If the value is one then profile 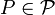 describes a possible input of web service
describes a possible input of web service 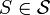 .
M is defined as follows:
.
M is defined as follows:
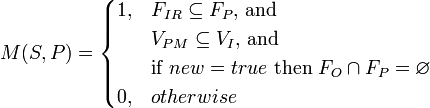
Example:
Profile 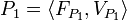 describes a possible input of service
describes a possible input of service 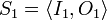 where:
where:
-
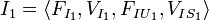 ,
,
-
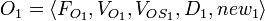
because:
-
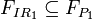 , i.e.
, i.e. 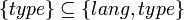 , and
, and
-
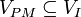 , i.e.
, i.e. 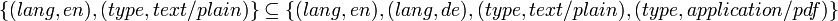 , and
, and
- the output is new i.e new1 = true.
Specialisation Function
A specialisation function 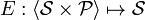 . E is defined as follows:
. E is defined as follows:
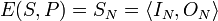 such that:
such that:
-
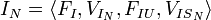 , where:
, where:
-
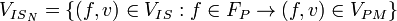 ,
,
-
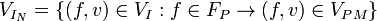 ,
,
-
and
-
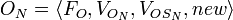 , where:
, where:
-
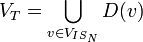 ,
,
-
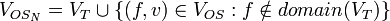 ,
,
-
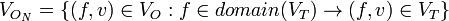 ,
,
-